Abstract
BACKGROUND: Ventilator-induced lung injury (VILI) requires repetitive transfer of energy from the ventilator to the compromised lung. To understand this phenomenon, 2 sets of equations have been developed to partition total inflation energy into harmless and hazardous components using an arbitrary level of alveolar pressure as a threshold beyond which further energy increments may become damaging. One set of equations uses premeasured resistance and compliance as inputs to predict the energy that would be delivered by typical ventilator settings, whereas the other equation set uses observed output values for end-inspiratory peak and plateau pressure of an already completed inflation.
METHODS: Our aim for this study was to compare the relative accuracy of these equation sets against the performance of a physical one-compartment model of the respiratory system, programmed with information readily available at the bedside and ventilated using both constant and decelerating flow profiles. Accordingly, equations of each set were compared against the corresponding energy areas measured by digital planimetry of pressure-volume curves for 76 ventilator and patient parameter combinations and over 500 power calculations.
RESULTS: With few exceptions, all equations strongly correlated with their corresponding measurements by planimetry.
CONCLUSIONS: This validation of threshold-partitioned energy equations suggests their potential utility for implementing practical strategies for VILI avoidance.
Introduction
Injuring lung tissue during ventilation requires recurring expenditure of energy.1 Conceptual and experimental links between energy delivery and parenchymal injury are becoming increasingly well understood.1,2,3,4 In the context of clinical ventilation, under passive conditions, the mechanical energy (work) of inflating the respiratory system is determined by the integrated sum of the instantaneous products of airway pressure and volume above baseline.5 Thus, the area of the airway pressure and volume plot quantifies inflation energy, and power is the energy imposed per time unit of any length. In most recent publications, power has been designated as the product of inflation energy per cycle, expressed in joules, and breathing frequency (breaths/min).5 On this time scale, power is measured in J/min. On a shorter time scale, power is expressed in watts, the equivalent of 1 J/s expended.
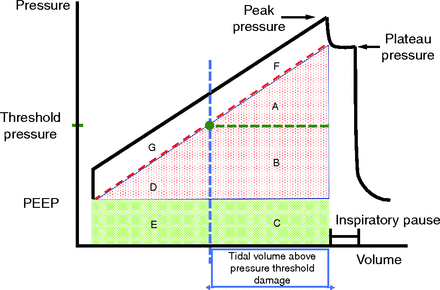
The total energy delivered by the ventilator per inflation cycle can be partitioned on the basis of the applied pressure (and resulting volume) into 3 components. These correspond to (1) the conserved elastic component of energy from which inflation begins (PEEP-related energy), (2) a driving elastic component of conserved energy that delivers the tidal volume, and (3) a resistive component of energy that dissipates during flow (Fig. 1). Note that not all inflation energy has damaging potential. Assuming passive conditions and that a force threshold must be met before damage occurs in the lung, these components can be further divided into threshold-partitioned energy components (Fig. 2). In prior work, using a simplified model that assumes unchanging compliance and resistance over the tidal range, 2 sets of equations were developed to calculate these threshold-partitioned components during constant inspiratory flow.5 One set of equations uses as inputs the premeasured resistance (R) and compliance (C) to predict the energy that would be delivered by the selected ventilator settings (titled predicted equations). The other equation set utilizes observed output values for end-inspiratory peak and plateau pressure at the end of inflation (titled observed equations). For each of the 2 equation sets, there are 7 equations to be considered (assuming the set damaging threshold for alveolar pressure exceeds PEEP). Defining dynamic pressures as PEEP inclusive, these equations are total power (blocks A–G of Fig. 2), total power above the pressure threshold (blocks A, B, C, F), total power increment above threshold (blocks A and F), total dynamic power (blocks A–E), dynamic power above threshold (blocks A, B, and C), total driving power (blocks A, B, and D), and driving power above threshold (blocks A and F).
Components of total inflation energy, which include the static elastic portion (influenced by PEEP), the driving elastic component (influenced by the driving pressure), and the flow-resistive component (influenced by airway resistance).
Threshold-partitioned energy component blocks. These subcomponents (A–G) are partitioned by the theoretical threshold pressure and the corresponding threshold volume (vertical line). Blocks E and C are subcomponents of the static elastic component. Blocks A, D, and B are subcomponents of the driving elastic component. Blocks G and F are subcomponents of the flow-resistive component. The circle indicates the alveolar pressure and volume that define the threshold point for damage to occur. All energy area combinations of interest can be estimated as outlined in our prior publication.5
In this study, the overall aim was to assess the accuracy and potential applicability of these descriptive algebraic equations for clinical use. As a first step, digital planimetry (pressure-volume area measurements) was used to determine the mechanical energy delivered by a ventilator to a test lung ventilated by constant and decelerating flows under different input conditions for resistance, compliance, and machine settings. The 14 equations for energy components were then compared to their corresponding planimetry measurements to test their validity in a physical, real-world application and to identify the conditions under which these estimates deviate significantly from those actually observed.
QUICK LOOK
Current Knowledge
Ventilator-induced lung injury requires repetitive transfer of energy from the ventilator to the compromised lung on each inflation cycle. In order for damage to occur, a stress/strain threshold must be surpassed beyond which further energy increments may become damaging.
What This Paper Contributes to Our Knowledge
This report validates, in a physical setting, key equations that characterize the energy and power delivered by the ventilator during passive inflation. Using input variables that are easily obtained at the bedside, these algebraic equations dissect the total inflation energy into components based on an assumed pressure threshold for damaging power.
Methods
To obtain data for this project, a Puritan Bennett 980 ventilator (Puritan Bennett, Pleasanton, California) was connected to a parameter-adjustable test lung (Model 1600 Dual Adult TTL, Michigan Instruments, Grand Rapids, Michigan). Different combinations of ventilator and patient parameters were tested to assess for discrepancy between estimates from our equations compared to area measurements by digital planimetry (Table 1). Equation estimates were tested for constant inflation flow using 4 types of air flow resistors: parabolic resistors (PneuFlo, Michigan Instruments) with nominal resistance values of 5 and 20 cm H2O, along with linear resistors (Hans Rudolf, Shawnee, Kansas) with nominal resistance values of 5 and 20 cm H2O, Equation estimates for various combinations of ventilator settings and patient parameters were then tested for decelerating flow using the same 4 resistors.
Combinations of Ventilator and Patient Parameters
For constant flow, the following combinations were applied using each of the 4 resistors. Baseline conditions were tidal volume 400 mL, PEEP 7.5 cm H2O, flow 0.5 L/s (ie, 30 L/min, yielding an inflation time of 0.8 s), breathing frequency 12 breaths/min, and compliance 0.05 L/cm H2O. Subsequently, one parameter was changed at a time. These changes included increasing PEEP to 15 cm H2O, decreasing breathing frequency to 10 breaths/min, increasing breathing frequency to 30 breaths/min, decreasing tidal volume to 300 mL, increasing tidal volume to 500 mL, increasing flow to 0.83 L/s (ie, 50 L/min), decreasing compliance to 0.02 L/cm H2O, and increasing compliance to 0.10 L/cm H2O. With constant flow, resistance was measured by the ventilator using an end-inspiratory breath-hold of 2.0 s.
Using decelerating flow, again with each of the 4 resistors, the following combinations of settings were used. Initial baseline settings and parameters were tidal volume 400 mL, PEEP 7.5 cm H2O, inspiratory time 0.8 s, breathing frequency 12 breaths/min, and compliance of 0.05 L/cm H2O. Subsequently, one setting was changed at a time. The changes were increasing PEEP to 15 cm H2O, decreasing breathing frequency to 10 breaths/min, increasing breathing frequency to 30 breaths/min, decreasing tidal volume to 300 mL, increasing tidal volume to 500 mL, increasing inspiratory time to 1.6 s, deceasing inspiratory time to 0.4 s, decreasing compliance to 0.02 L/cm H2O, and increasing compliance to 0.1 L/cm H2O. Because resistance changes over time in decelerating flow (especially when using the parabolic, orifice resistors), an average resistance was needed for calculations. This average resistance estimate was obtained by first switching to constant flow using the same parameters and inspiratory time and then performing an end-inspiratory breath-hold.
In order to obtain the per cycle energy estimates, the appropriate values were first inputted into each equation. The output was then multiplied by frequency to provide a power/min calculation in units of L × cm H2O/min. Since 1 J approximates the product of 1 L × 10 cm H2O, those mathematical power calculations were then converted into conventional J/min by dividing them by 10.
Planimetry for Actual per-Cycle Inflation Energy
Under constant flow conditions, time is a linear analog of volume. Consequently, when testing constant flow, planimetry of the pressure-time relationship displayed on the ventilator, which is represented schematically as Figs. 1 and 2, provides reasonably accurate measurement of all energy components. However, this study also assessed decelerating flow, for which a pressure-time plot is not analogous to the needed pressure-volume area. On many ventilators, including the Puritan Bennett 980, the needed relationship of volume to pressure is a display option inscribed with volume on the y axis and pressure on the x axis. Using this configuration, the mechanical energy components can be delineated for any volume delivery pattern, including those resulting from constant or decelerating flow (Fig. 3).
Threshold-partitioned energy component blocks of a volume-pressure graph. Blocks A–G correspond to the same blocks as in Figure 2. Blocks E and C are subcomponents of the static elastic component. Blocks A, D, and B are subcomponents of the driving elastic component. Blocks G and F are subcomponents of the flow-resistive component. The circle indicates the alveolar pressure and volume that define the threshold point for damage to occur.
Pressure-volume loops were recorded for each test via the image capture function on the Puritan Bennett 980 ventilator. The portions of these pertaining to inflation were then input into the Microsoft Paint (Microsoft, Redmond, Washington) application. The image length and width ratios were scaled so that a length of 10 cm H2O (x axis) was made equal to the length of 1 L (y axis). The area corresponding to 1 L on the volume axis by 10 cm H2O on the pressure axis quantifies 1 J of energy. Lines were drawn using the Microsoft Paint application to outline the different pressures: PEEP, threshold, peak, and plateau. A straight line was drawn from the plateau pressure to PEEP to distinguish the flow-resistive energy component from the elastic ones. The intersection of the arbitrarily set elastic threshold pressure with this line allowed for delineation of the different energy blocks. Each image was then uploaded into planimetry software (SketchAndCalc, Icalc, Palm Coast, Florida) where the pressure-volume areas of all energy blocks were individually measured. The measured area for one respiratory cycle (one inspiratory loop) is the corresponding energy in J. These values were then multiplied by breathing frequency to obtain the relevant power component, expressed in J/min.
Statistical Analysis
The effects of ventilator settings on the deviations of observed and predicted equation estimates from actual planimetry measurements were evaluated using linear models with main effects terms for each setting. The variability across ventilator settings of deviations of predictive and observed equations obtained from planimetry measurements was compared for constant and decelerating flow conditions using the F test. In both analyses, deviations from planimetry were analyzed on the log2 equation-to-planimetry ratio scale. Agreement among observed equations, predicted equations, and planimetry measurements was visualized using radar plots. Analyses were conducted using R version 4.36 (R Foundation for Statistical Computing, Vienna, Austria), which includes the package fmsb version 0.7.0.7
Results
To assess their accuracy, calculations from the observed energy equations (using observed value outputs, ie, peak pressure, plateau pressure) and the predicted energy equations (using input values, ie, rate of flow, resistance, compliance) were compared to planimetry-determined actual values. In general, all 14 equations demonstrated strong correlations with the planimetry calculations. Radar charts were used to plot the absolute values of power measurements for each combination of parameters, as calculated by the 2 equation types and planimetry. On these displays (one display for each energy element of interest), each axis indicates a different patient and ventilator combination, starting from the baseline settings in the top left. Overlap in the 3 values for a combination indicates agreement between equations and planimetry. A sample radar plot showing 2 power measurements (total power and dynamic power above threshold) using the observed and predicted equations and planimetry measurements demonstrates strong agreement for all settings and parameters (Fig. 4). Additional radar plots of all power measurements, for each equation set, for constant and decelerating flow, outlining all the tested combinations of ventilator and patient parameters are available in the supplement. These demonstrate strong agreement between both types of equation and actual planimetry (Supplement 1, see the related supplementary materials at http://rc.rcjournal.com/).
Radar plots showing power measurements (in J/min) for total power above threshold (A and B) and dynamic power above threshold (C and D) with constant and decelerating flow. The red line outlines the calculations based on observed value outputs. The green line outlines the calculations based on input values predicted. The blue line outlines the actual measurements using planimetry. The combinations of patient and ventilator parameters were tested with 4 air flow resistors: parabolic resistors with a resistance of 5 cm H2O (P5) and a resistance of 20 cm H2O (P20) and linear resistors with resistance values of 5 cm H2O (L5) and 20 cm H2O (L20). The baseline tests with each resistor are in the top left of each radar plot. One variable was then changed with each subsequent test (Table 1). The type of resistor and the change from baseline are indicated next to its corresponding power values. The changes are listed in counter-clockwise order. PEEP = positive end expiratory pressure (cm H2O). RR = respiratory rate (breaths/minute); TV = tidal volume (L);FR = flow rate (L/s); C = compliance (L/cm H2O).
Of the 532 power estimates that were compared to planimetry measurements, only 3 had an absolute value deviation of > 5 J/min. These were (1) the predicted equation for total power above threshold with constant flow, a linear resistor of 20 cm H2O, and breathing frequency increased to 30 breaths/min from the baseline rate of 12 breaths/min (underestimated by 6 J/min, equation to planimetry ratio of 0.75); (2) the predicted equation for total power above threshold with decelerating flow, a linear resistor of 20 cm H2O, and breathing frequency increased to 30 breaths/min from the baseline rate of 12 breaths/min (underestimated by 7.5 J/min, equation to planimetry ratio of 0.72); and (3) the predicted equation for total power increment above threshold with decelerating flow, a linear resistor of 20 cm H2O, and breathing frequency increased to 30 breaths/min from the baseline rate of 12 breaths/min (underestimated by 6 J/min, equation to planimetry ratio 0.63). In each of these instances, a linear resistor of 20 cm H2O and a high breathing frequency of 30 breaths/min were used. The auto-PEEP values generated with this combination was 3.2 cm H2O in constant flow and 3.0 cm H2O in decelerating flow. In comparison, auto-PEEP in all other combinations ranged from 0–0.6 cm H2O. Since the value inputted into the predictive equations was the set PEEP, rather than the (higher) total PEEP, the equations underestimated the power measurement. When correcting for auto-PEEP, the difference from planimetry declined from 6.0–5.6 J/min for instance (1), 7.5–4.1 J/min for instance (2), and 6.2–1.0 J/min for instance (3).
A variance comparison analysis was used to detect signals of deviation depending on flow type (constant vs decelerating), equation type, and testing combination used (Supplement 2, see the related supplementary materials at http://rc.rcjournal.com/). No equation type (eg, total, power, total power above threshold) caused a consistent deviation from the planimetered value. Neither the observed nor predicted equations caused consistent deviations from planimetry, indicating equal reliability. As noted above, compared to constant flow, decelerating flow caused a statistically significant (P < .05) greater deviation in 3 instances out of 14. These were in the observed equation of total power (constant flow SD 0.07 [95% CI 0.06–0.09] vs decelerating flow SD 0.17 [95% CI 0.14–0.22]), the observed equation of total power above threshold (constant flow SD 0.11 [95% CI 0.09–0.14] vs decelerating flow SD 0.17 [95% CI 0.14–0.22]), and the observed equation of total power increment above threshold (constant flow SD 0.17 [95% CI 0.13–0.22] vs decelerating flow SD 0.46 [95% CI 0.38–0.59]). In contrast, compared to decelerating flow, constant flow caused a statistically significant greater deviation in just one instance out of 14, the observed equation of driving power above threshold (constant flow SD 0.17 [95% CI 0.14–0.23] vs decelerating flow SD 0.14 [95% CI 0.11–0.18]).
Linear models were used to examine if a specific change in ventilator or patient variable (ie, type of resistor, increase or decrease in PEEP, breathing frequency, compliance) caused a consistent deviation from the planimetry measurements (Supplement 3, see the related supplementary materials at http://rc.rcjournal.com/). In both constant and decelerating flow, no specific variable change caused a consistent deviation from the planimetered value.
Discussion
The delivery of damaging power by the mechanical ventilator is an evolving model to explain ventilator-induced lung injury (VILI).1-4 Although both correct and useful for some purposes, unmodified calculations of total power based on the product of inflation energy per cycle and breathing frequency may not be precise enough to predict VILI risk since different combinations of ventilator settings (eg, volume, frequency, PEEP) may deliver the same total power without carrying equal risk of damage.8,9 Partitioning the components that contribute to total energy per cycle and power may be necessary to understand which elements are critical to VILI causation. Exactly which component or subcomponent of elastic energy, driving or dynamic, correlates best with tissue damage has not been clearly identified. Nor has the amplifying effect of flow and waveform been clearly identified. The threshold of alveolar pressure at which the hazard emerges for a given lung unit is very likely to vary with its innate vulnerability and its local environment within the lung.
Overall, the equations demonstrated excellent accuracy. Only 3 out of 532 estimates had an absolute difference exceeding 5 J/min compared to planimetry. These deviations, which occurred in predicted equations, emerged in part due to gas trapping at high frequency (note here that total PEEP is not a reliably predictive input value but can only be determined post facto). We presume but cannot prove that other contributors to these aberrancies relate to the interaction of the ventilator flow delivery algorithm and the mechanical circuit setup under these specific conditions. None of the 14 equations caused consistent inaccuracy in calculations across the tested conditions. Decelerating flow caused statistically significant greater SD compared to constant flow but only for 3 of the 14 equations. Greater deviation in decelerating flow might have been anticipated, as the equations were originally designed for constant flow circumstances. In general, however, the decelerating flow equations performed with sufficient accuracy for potential clinical applications. The data were also interrogated to determine if a change in a specific parameter resulted in a consistent deviation from the planimetry measurements of energy and power components. None did; no parameter change was responsible for a consistent pattern of imprecision. This accuracy is clinically relevant, as the equations performed well despite being challenged by a wide range of simulated circumstances and machine settings.
Limitations
Any mechanical simulation does not perfectly replicate biological conditions of the diseased lung. Consequently, however good the equation system, the VILI risk associated with any ventilatory pattern can only be approximated. For example, in a biological system, as opposed to a purely mechanical one, 2 seldom considered and time-dependent factors that relate to flow and repetition of monotonous and unchanging settings are stress focusing and power concentration within a shrinking air space.1,4,10 Neither is considered by our equation system. Moreover, the limitations of arbitrarily assigning a single threshold pressure have been discussed in prior work.1,5 It seems appropriate to note here, however, that for the lungs of ARDS a numerical pressure threshold for damage initiation (10 cm H2O or 20 cm H2O in our simulation) likely exists for some of their units, with vulnerability varying with gravitational plane, surrounding interstitial pressure, and local tissue distortions.11 This work provides validation for a conceptual framework from which future research may delineate threshold pressures in a biological setting; experimental studies are needed to elucidate possible thresholds in various disease states. Our modeling does not incorporate pressure threshold variations that would be expected to occur with changes of patient positioning and disease severity.
Conclusions
This report validates in a physical setting our pressure threshold-partitioned energy/power equations relevant to VILI. These simplified estimates provide quantification based on input variables readily measured under passive conditions in clinical settings, either before or after implementation of the ventilatory prescription. As algebraic expressions, these modeling equations conceivably may be programmed into ventilator software to estimate, display, or track progression of delivered energy and power at the bedside.
Footnotes
- Correspondence: John J Marini MD, Division of Pulmonary, Allergy, Critical Care, and Sleep Medicine, University of Minnesota, 420 Delaware SE, MMC 276, Minneapolis, MN 55455. E-mail: Marin002{at}umn.edu
See the Related Editorial on Page 277
Supplementary material related to this paper is available at http://rc.rcjournal.com/.
The authors have disclosed a relationship with Medtronic.
This research was supported by the National Institutes of Health’s National Center for Advancing Translational Sciences, grant UL1TR002494.
This research was conducted at Regions Hospital, Saint Paul, Minnesota.
- Copyright © 2022 by Daedalus Enterprises