Abstract
Redirection of our clinical attention from the pressures and volumes of the individual cycle to the broader and more inclusive considerations of energy load and power has untapped potential to reduce iatrogenic risk from ventilation (ie, ventilator-induced lung injury). Power is the product of breathing frequency and inflation energy per breath. Yet, while feasible to calculate at the bedside, measuring total power may not prove to be precise enough for accurate prediction of ventilator-induced lung injury, even if normalized to lung capacity (ie, specific power). The same power value can be reached by a multitude of frequency and tidal volume combinations, not all of which carry equal risk of damage. If some arbitrary level of alveolar pressure were accepted as a sharply defined hazard boundary, a rather straightforward geometric analysis theoretically would allow partitioning of overall tidal energy into components above and below a damage threshold. In this discussion, we introduce the concept of quantitative power partitioning and illustrate how tidal energy and power might be deconstructed into their key parts.
Introduction
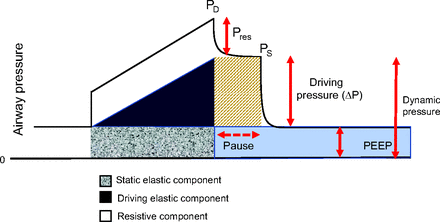
Mechanical energy is defined as the product of an applied force and the distance (or length) moved in response to that force. Energy expenditure, therefore, implies motion and displacement. Translated into the context of passive ventilation, energy is a pressure-volume product: pressure is force divided by area and volume is area multiplied by length. Multiplying pressure by the volume it displaces, therefore, yields a force-length product (ie, energy) that can be graphically depicted and quantified as a pressure-volume area (Fig. 1). Multiplication of energy per cycle by ventilating frequency yields inflation energy per minute, which is a measure of power.
Inflation areas that make up the total inflation energy. These correspond to the simplified equation of motion: Ptot = (Pres + driving pressure [ΔP] + PEEP). Dynamic pressure is defined as the sum of PEEP and driving pressure. PD = peak dynamic pressure; Pres = resistive pressure; PS = plateau pressure.
Energy, Power, and Tissue Injury
Injuring lung tissue by the mechanical forces of ventilation (ie, ventilator-induced lung injury [VILI]) requires recurring energy expenditure.1,2 Importantly, as time passes, tissue adaptation also proceeds as high-stress/high-strain tidal cycles are repeated. Whether it is power or the cumulative number of intolerably high-strain cycles (proportional to [power × duration]) or a combination of both that matters most to VILI expression has not yet been clarified. Because internal strains experienced within the injured lung cannot be directly measured, lung-protective approaches currently focus on the global variables that can be easily measured externally by clinicians, such as pressures, flows, and volumes.3,4 The loading rate of inflation energy is reflected in the power calculation. The term “power” indicates the rate of energy expended per time unit of any length (seconds, minutes, or hours). When applied to mechanical ventilation, power is currently understood in the clinical setting as the energy per minute (J/min), which is obtained by multiplying the energy per inflation cycle delivered by the ventilator multiplied by the breathing frequency.
Energy per cycle (synonymous with “work”) is the product of pressure applied above the fully relaxed baseline (ie, atmospheric pressure) and the resulting volume change.5 On a plot of applied pressure versus inflation volume, geometric areas quantify the contributors to tidal energy (Fig. 1).6 Inflation energy has 4 components: tidal volume and 3 pressures that relate to flow resistance, respiratory system elastance, and the end-expiratory pressure platform from which inflation begins; ie, energy equals the tidal volume multiplied by the sum of resistive pressure (Pres), driving pressure (ΔP), and PEEP: energy = VT × (Pres + ΔP + PEEP). By adding a fifth component, the breathing frequency (f), the mechanical power is obtained: power = f × VT × (Pres + ΔP + PEEP).
Do Flow-Related and PEEP-Related Energy Matter?
The inclusion of flow-resistive pressure and PEEP in our conceptual analysis of strain, energy, and power invites some explanation. Although a considerable proportion of flow-resistive energy is indeed spent in moving gas through the endotracheal tube and conducting airways, rapid rates of inflation simultaneously accentuate micromechanical stresses at the parenchymal level, especially in vulnerable alveolar units within the mechanically heterogeneous, diseased lungs of individuals with ARDS.
The end-expiratory pressure, too, continues to stimulate controversy in discussions of lung protection and energetics on several fronts. PEEP bears a U-shaped relationship to VILI risk, with low levels tending to reduce atelectasis, distribute stress, and reduce the maximum strains experienced by the lung units most predisposed to mechanical injury. Pushed above that helpful level, however, higher PEEP sets an elevated platform from which widespread tidal overstretching of the parenchyma may outweigh the benefits of further recruitment. Although that adverse potential is generally acknowledged, the relevance of PEEP to damaging inflation energy has been questioned on the basis that the same pressure baseline is eventually restored at the end of deflation. Yet, because PEEP undeniably elevates volume and global strain over the resting values of their fully relaxed states, raising PEEP requires each inflation volume increment be achieved at higher absolute pressure and therefore requires greater energy input from the ventilating source. Thus, the driving pressure (ie, tidal elastic) component of inflation energy (ΔP × VT) parallels the amplitude of tidal volume but only quantifies incremental work due to raising elastic pressure above baseline PEEP. Calculations of total inflation energy, therefore, also must incorporate the PEEP × VT product.
Does Total Power Measured From Airway Pressure and Flow Parallel VILI Risk?
Whereas the linkage between total power and lung injury risk is relatively well established, it is debated whether all combinations that sum to the same power value incite equal damage for the individual patient.7,8 Recent experimental data suggest that, indeed, this may be the case when high, VILI-inducing power levels are sustained for long enough periods.9 Whatever its components, the same numerical value of total power calculated from airway pressure implies different hazards for different patients. The chest wall, for example, also requires energy and power to expand, and its compliance is degraded by massive obesity.10 Just as importantly, when seeking to quantify damaging potential of power, the externally measured power stimulus—even one based on transpulmonary pressure—must be referenced to the capacity of the open air space exposed to it; tidal energy distributed into a normal lung generates less strain than it does within a lung of lesser capacity. In ARDS, therefore, the injuring potential of a fixed value of power should be adjusted for the size of the “baby lung” that can accept it.11
Relationships Among Strain, Stress, Energy, and Mechanical Power
At the outset, it is important to define the physical terms used in the following discussion (Table 1). Generally speaking, mechanical strain of any material is defined as the change in length relative to its resting length (ie, deformation or stretch) that is produced by an external force. Strain is always associated with a force that develops within the deforming structure that is equal but oppositely directed to the force that produced it.12 In other words, the reactive counterforce (stress) balances the one causing strain. For the lung, external forces that cause changes from the resting volume (V0) result from applied pressures: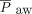 
when referring to the total respiratory system or transpulmonary pressure when referring to the lung. Because energy is defined as mean airway pressure, 
× ΔV and strain is ΔV/V0, it follows that (strain × 
) = ([ΔV ×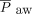 
]/V0), that is, the energy normalized to the volume to which it is applied. When discussing possible thresholds of damaging strain, therefore, it must be understood that these cannot be isolated from the stress and energy that cause them. Finally, by definition, the product of (stress × strain × f) represents the power applied to the lung in 1 min (J/min/mL).
Definitions of Physical Terms
How Important Is Stretch?
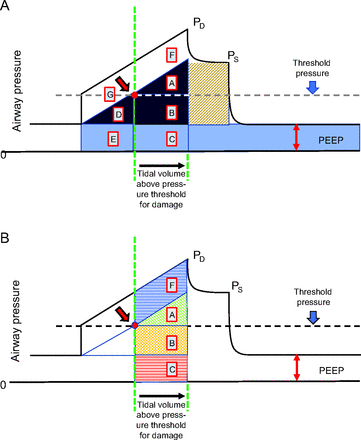
Even if fundamentally related to VILI, measuring power normalized to lung capacity (ie, specific power) may not be enough for accurate VILI prediction. Quite reasonably, it has been suggested that, for any individual patient, excessive strain per inflation cycle may be a co-requisite with size-normalized power for damage to occur.13 In other words, a threshold of stress/strain (sharp or indistinct) may need to be crossed before the applied energy contributes to injury. If that presumption proves true, it follows that, during each breath, some of the delivered inflation energy would not contribute to damage; rather, only the energy that crosses the critical stress/strain boundary would do so (Fig. 2). Thus, the first increments of VT and pressure development are intuitively less damaging than those that occur later in the inflation. Following this premise of alveolar pressure threshold dependence, vulnerabilities of different lung sectors would vary depending on their local transpulmonary pressures. Indeed, the current clinical practice of constraining plateau and driving pressures, though centered only on the individual tidal cycle, is tacitly underpinned by the implicit mandate to avoid excessive stress and strain.14
A: Energy component blocks (A–G) partitioned by the alveolar threshold pressure and its corresponding threshold volume (green vertical line). Capital letters correspond to the areas partitioned by the injury threshold pressure and volume and the components related to flow-resistive, tidal elastic, and total PEEP energy. The dashed lines indicate the pressure and volume thresholds. The thick red arrow indicates the alveolar pressure and volume that defines the threshold point for damaging stress and strain. B: Potential contributors to damaging energy. Once the pressure threshold is crossed (green dashed line), all patterned areas (A, B, C, and F) may become important. Alternatively, only energy increments above the threshold pressure (ie, areas A and F) may hold damaging potential. All energy area combinations of interest can be estimated (Table 2). Areas below the pressure threshold and their associated volumes are assumed not to contribute to damage. The red arrow with the red dot indicates the alveolar pressure and volume that defines the threshold point for damaging stress and strain. Capital letters correspond to the areas partitioned by the injury threshold pressure or volume dashed lines and the components related to flow-resistive, tidal elastic, and total PEEP energy. PD = peak dynamic pressure; PS = plateau pressure.
Cautions Regarding the Threshold-Partitioned Model
In any attempt to identify and quantify the essential elements of damaging energy, it must be understood that the concept of mandatory crossing of an injury threshold is purely hypothetical and rather complex. For example, whether such a threshold relates to stress/strain, tidal cycle energy, power, ventilatory duration, or all of these is simply unknown and speculative. Yet if some arbitrary level of alveolar pressure were accepted as a sharply defined hazard boundary (eg, based intuitively on intolerable stretch and fracture of weak microfibrils of the extracellular matrix), a rather straightforward geometric analysis would theoretically allow partitioning of overall tidal energy into prethreshold and postthreshold components (Fig. 2). Again, such an admittedly simplistic attempt to assign and quantify VILI risk to selected portions of the applied energy requires the designation of an arbitrary strain threshold that is proportional to the stress level (reflected by alveolar pressure) at which injury becomes possible. That stress/strain threshold of a given lung unit would undoubtedly vary by the site within the lung (eg, influenced by its gravitational dependence). The injury threshold also would depend upon the vulnerability of the lung to damage by mechanical stretching forces and on the stage of illness. To illustrate, the lungs of large animals are inherently less easily damaged than are those of small animals.15,16 Moreover, whatever the species, healthy lungs resist damage robustly, whereas pre-injured lungs appear more vulnerable, likely due primarily to micromechanical stress amplifiers such as accentuated viscoelastic drag, among others.12,15
Implementing the Partitioning of Energy and Power
With such simplifications and assumptions in mind, a conceptual framework for quantitative energy partitioning can be constructed using bedside-measured variables. This breakdown is most easily envisioned and illustrated assuming inflation by constant flow. Note that energy calculations made under such constant-flow conditions approximate (or may slightly underestimate) those relevant to the decelerating flows of more commonly used pressure-targeted modes as well as the ramp profile of volume-targeted flow control.17 Although the flow-determined rate of parenchymal expansion certainly affects the actual tissue strains experienced on the local level by micromechanical forces, the global stress that most directly determines parenchymal strain is reflected in the externally measured pressures comprising elastic recoil (static and so-called dynamic): total elastic pressure = [PEEP + ΔP]. Therefore, although flow contours differ for decelerating and constant-flow profiles, energy calculations for the latter approximate the minimum expended against recoil forces.17 In the discussion, figures, and equations that follow, it should be understood that pressure may refer interchangeably either to passive airway pressure that distends both lung and chest wall or only to the transpulmonary pressure applied across the lung. The corresponding energy and power calculations reflect those pressure inputs. Although the transpulmonary pressure is of most direct interest to the lung and VILI hazard, pleural pressure (estimated with esophageal pressure) is infrequently measured in current clinical practice.18,19
The Constant-Flow Model
Under constant-flow conditions, time is an analog of volume. Once the simplifying assumptions outlined above are made, energy per tidal inflation can be computed from geometric pressure-volume areas and from the simple algebraic formulas that define them.6 If resistance (R) and compliance (C) are both known and held constant over the range of the applied VT, energy components of interest can be estimated from the clinician-specified inputs for the ventilating cycle (ie, VT, PEEP, and flow) as soon as a threshold for injuring pressure is assumed to exist and assigned (Table 2). These correspond to the energy sub-block areas graphically displayed on a plot of applied pressure and resulting volume (Fig. 2).
Equations for Energy Components Using Observed Value Outputs and Input Values Predicted From Mechanical Parameters
It must be acknowledged that, although cumulative energy load and total power have been experimentally or clinically linked to VILI, exactly which delivered component or subcomponent of power correlates best with damage has not been clearly identified.9,20,21 For example, it might be argued that only energy that relates to driving pressure or total elastic pressure {ie, the product of volume and absolute alveolar pressure, or (VT × [ΔP + PEEP])} would best track lung stretch and VILI risk.13 Alternatively, the total kinetic energy applied in excess of PEEP {ie, the product of volume and the sum of ΔP + Pres. ie, (VT × [ΔP + Pres])} might hold equal interest regarding the potential to generate inflammatory changes. Furthermore, perhaps only energy components that exceed that pressure level for damage (ie, threshold pressure), would be VILI-relevant. Such a threshold might reside anywhere within the pressure range that envelops the tidal cycle (ie, from zero to peak dynamic pressure), or even above it. The geometric partitions and their corresponding equations will vary depending on whether the threshold pressure lies within the range of driving pressure. Examples of such calculations are provided in Table 3. As the search to define the safety limits of power application proceeds, one or more of these energy sub-blocks may eventually sharpen the precision of target setting for lung-protecting power.
Example Calculations for Energy Components at Various Threshold Pressures
Adjusting for Aerated Lung Volume
There is no simple way to accurately assess the dimensions of the open baby lung subjected to inspiratory power at the bedside. Gas dilution methods can be implemented for research purposes and have been incorporated into at least one commercially available mechanical ventilator (Carestation, GE Healthcare, Chicago, Illinois). Unfortunately, equipment availability is limited, gas dilution measurements require some time to complete, and data, while generally helpful, are of unproven accuracy in cases of ARDS.22,23 Because measurements of tidal respiratory-system compliance tend to reflect the number of lung units more closely than their stiffness, it has been suggested that the ratio of observed compliance to the predicted value could offer a reasonable size adjustment (ie, a power-concentrating factor for calculations) that is applicable to all patients.11 Unfortunately, there is good reason to believe that this practical compromise also may be based on flawed assumptions of unchanging and equal compliances of open lung units.
Clinical Implications and Limitations of the Method
Quantitative partitioning of inflation energy might help in the implementation of a lung-protective strategy with an undeniable justification rooted in the fundamentals of physics. The theoretical impact of a proposed change in the ventilatory prescription on the components of the energy/power complex could then be numerically estimated before they are actually made. Using similar principles when only currently measured pressures, flow, volume, and frequency are at hand, a comparable rationale and method can produce condensed formulae that estimate these same energy elements (Table 2, Table 3). This would characterize the pattern already in use and could track serially the evolution and resolution of the ergo-trauma determinants of greatest interest.
All components of these simplified equations are measurable at the bedside except for threshold pressure, which must be arbitrarily assigned. In concept, the energy difference resulting from a change in ventilation pattern can be rather easily estimated or monitored—even automated—for bedside use. Undeniably, however, the thresholds for applied pressure on which energy partitioning is based (if they exist at all) are likely to differ site by site within the heterogeneous lung.24 A pressure threshold also would be expected to vary with body positioning, injury severity, and stage of acute illness. It is worth emphasizing here that multiple thresholds may exist for VILI expression, other than measurable airway or transpulmonary pressure, such as energy delivered per minute (power) or duration of high-energy ventilation.
There are other concerns. For decelerating (as opposed to constant) flow profiles (ie, those that characterize pressure-targeted modes), these equations provide only good approximations. Moreover, however useful (or unnecessary) such equations might turn out to be, they do not take into account all potentially damaging stresses that occur within the lung. For example, all stored end-inspiratory energy is released during expiration—indeed, expiration is the only thing that the so-called driving pressure (ie, the difference between plateau pressure and PEEP) actually drives. Although neglected in practice, this deflation energy also may contribute to injury, but to an as yet undetermined degree.25,26 Nonetheless, whatever the importance of expiration might be, the easily quantified end-inspiratory potential energy sets the upper bound for the damaging deflationary energy of the tidal cycle.
Summary
Undoubtedly, redirection of our narrowly focused attention from the pressures and volumes of the individual cycle toward energy load and power has untapped potential to reduce iatrogenic risk from ventilation.2 With all its limitations, the admittedly basic and airway pressure-based quantitative approach that we propose here represents a conceptual first step toward refining the utility of ventilation power for direct clinical use. Because energy is required to inflict damage, heightened awareness of energy and power and their key components appeals to mechanistic logic. Delving into the energetics of VILI makes particular sense because energy determinants can be estimated using parameters routinely measured at the bedside. However, the relative place of power among currently used static tidal characteristics (eg, plateau pressure, driving pressure) is still actively debated.7,8 Whether further partitioning of total power adds clinical value to our current practice requires prospective experimental verification and remains to be determined.
Footnotes
- Correspondence: John J Marini MD, Regions Hospital, MS11203B, 640 Jackson St, St. Paul, MN 55101. E-mail: marin002{at}umn.edu
The authors have disclosed no conflicts of interest.
- Copyright © 2020 by Daedalus Enterprises
