Research ArticleOriginal Research

Using Statistical Techniques to Predict Dynamic Arterial PCO2 in Patients With COPD During Maximum Exercise

Ming-Lung Chuang, I-Feng Lin, Janine RE Vintch and En-Hao Tien
Respiratory Care July 2012, 57 (7) 1106-1114; DOI: https://doi.org/10.4187/respcare.01320

Abstract

BACKGROUND: PaCO2 as measured during exercise in patients with COPD is poorly predicted (predicted PaCO2) from lung function testing and some noninvasive measurements, such as end-tidal PCO2 (PETCO2).

OBJECTIVE: We performed a number of statistical techniques on PETCO2 and its interaction with other physiologic variables during exercise testing, in order to improve our ability to predict PaCO2. The estimated PaCO2 as determined from these techniques may therefore be used to contrast the PETCO2 readings that are measured during an incremental exercise test on a breath-by-breath basis (ie, PaCO2 – PETCO2), and to identify exercise-induced hypercapnia.

METHODS: Forty-seven men with COPD underwent both pulmonary function testing and incremental exercise testing until limited by symptoms. Arterial blood gases and exercise physiological measurements were performed during maximal exercise testing. The prediction equations for PaCO2 were generated using regression techniques with the leave-one-out cross-validation technique.

RESULTS: Forty-one patients were included in the final analysis after 6 patients were excluded due to inadequate data collection. The best prediction equation we found was: predicted PaCO2 = 23.71 + PETCO2 × (0.9–0.01 × DLCO –0.04 × VT) – 2.61 × SVC – 0.04 × MEP, where DLCO is diffusing capacity for carbon monoxide in mL/min/mm Hg, VT is tidal volume in L, SVC is slow vital capacity in L, and MEP is maximum expiratory pressure in cm H2O. The difference between the measured and predicted PaCO2 at each time point was not statistically significant (all P > .05). The standard errors of the estimated PaCO2 at each time point were 0.91–1.12 mm Hg.

CONCLUSIONS: A validated mixed-model regression derived equation yields a predicted PaCO2 trend during exercise that can be helpful when interpreting exercise testing to determine PaCO2 – PETCO2 and exercise-induced hypercapnia.

Introduction

Arterial PCO2 (PaCO2) is governed by integrated alterations in minute ventilation (V̇E), physiologic dead-space to tidal-volume ratio (VD/VT), and carbon dioxide output (V̇CO2) (ie, Bohr equation). Exercise-induced hypercapnia (EIH) is a sign of inadequate ventilation that is due to a number of physiologic changes in a patient with COPD, including hyperinflation, reduced gas exchange capabilities (ventilation/perfusion mismatch), increased VD/VT, and more rarely the opening of a right-to-left shunt.1,2 It is important to detect the development of EIH in this patient population so that we may appreciate its mechanisms and consider additional management strategies.

PaCO2 is highly variable and is poorly predicted from resting lung function testing.3,4 While there are noninvasive tools2,5,6 to measure this parameter, there are many technical limitations6,7 or conditions, such as anesthesia, mechanical ventilatory support,8–10 old age,11,12 or COPD,13 that impact its measurement. The diagnosis of EIH or increased VD/VT is invasive and requires an arterial line. The multiple arterial blood gas measurements that may be drawn to determine the VD/VT are also costly.

The inaccuracies of estimating a predicted PaCO2 can be improved by considering end-tidal PCO2 (PETCO2) plus VT in normal adults14 or FEV1 plus VT in patients with COPD.3 Other factors, such as exertional hyperinflation, weakened inspiratory muscles, and deranged neuroregulatory control, may also have an impact on EIH.1 Therefore we assumed that it would be too difficult to improve the accurate predicting of PaCO2 by conducting any further physiological studies. We then hypothesized that by recruiting more physiological variables for statistical analysis our ability to predict PaCO2 would be improved in adults with COPD.

The study was designed to identify variables for deriving equations that would more accurately estimate PaCO2 trends in patients with COPD during maximum exercise testing. The clinicians can compare the PETCO2 trend of the popularly used 9-panel plot breath-by-breath15 with the equation-derived estimated PaCO2. A clinician's ability to detect reduced alveolar ventilation and gas exchange capabilities in patients with COPD could be enhanced by this information.

QUICK LOOK

Current knowledge

PaCO2 is difficult to predict from noninvasive measures in patients with chronic lung disease during exercise testing. Alterations in ventilation/perfusion complicate this prediction.

What this paper contributes to our knowledge

The best prediction equation for PaCO2 was a mixed model regression technique that included PETCO2 slow vital capacity, maximum expiratory pressure, diffusing capacity for carbon monoxide, and tidal volume. The best way to ascertain exercise induced hypercapnia, the difference between PaCO2 and end-tidal CO2, or the ratio of dead space to tidal volume remains analysis of arterial blood.

Methods

Forty-seven patients, age 50–76 years, with COPD of varying severity, based on the Global Initiative for Chronic Obstructive Lung Disease (GOLD) criteria,16 were enrolled to participate in this study. All subjects were clinically stable out-patients receiving a regular schedule of orally administrated or inhaled bronchodilators, with or without oral prednisolone of < 10 mg per day. Patients with substantial underlying arrhythmias, a history of malignancy, diabetes mellitus, cardiovascular or peripheral vascular disease, or locomotion problems were excluded from the study. The patients did not participate in any physical training protocol. However, regular activity was not limited. The exercise protocol and procedure, as well as the risks of maximal exercise testing, were explained. The institutional review board approved this study, and all subjects gave their consent to participate.

To derive equations for predicting PaCO2 trends, we prospectively collected lung function and exercise data, utilizing multiple arterial blood gas analyses from patients with COPD, while they were at rest and while performing a ramp-pattern exercise testing protocol. Several steps of model screening were performed to select candidate equations. Both goodness-of-fit measures and cross-validation techniques were used to assess the model's validity. Because of the invasiveness of inserting an arterial line, the cost of multiple arterial blood gas analyses, and limited study subjects, a leave-one-out cross-validation was performed, instead of recruiting another large sample to validate the equation. (See the statistical analysis section.)

Pulmonary Function Testing

To select eligible subjects for this study we used spirometry to evaluate the severity of air-flow obstruction. For a detailed description of the lung function test performed, please refer to the study by Chuang et al.17 The lung function test was performed before exercise testing and included maximally forced expired flow curves, lung volumes, maximum voluntary ventilation, and diffusing capacity for carbon monoxide (DLCO) (6200 Autobox DL, SensorMedics, Yorba Linda, California). Maximum inspiratory pressure was measured at residual volume (RPM, Micro Medical, Rochester, Kent, United Kingdom). Maximum expiratory pressure was measured at total lung capacity. Maximum inspiratory pressure and maximum expiratory pressure were each performed 3 times with a one-minute recovery period between efforts. The best result was recorded for analysis.

Maximal Cardiopulmonary Exercise Test

Stable exercise gas exchange was initially obtained while the subject sat at rest on the cycle ergometer (CardiO2, Medical Graphics, St Paul, Minnesota). Data were collected during a 2-min period of rest, followed by a 2-min period of unloaded cycling, followed by a ramp-pattern cycle ergometer exercise test to exhaustion. The work rate was increased at a rate of 5–20 watts per minute, according to the subject's individual fitness. The rate of increase was selected so the subject was able to complete the test within approximately 10 min.18,19 Oxygen uptake (V̇O2) (mL/min), CO2 production (V̇CO2) (mL/min), and V̇E (L/min) were computed breath by breath, and the data were displayed every 15 seconds, using an on-line computer program. We designated the V̇O2max as the peak or maximum V̇O2 that the patient achieved. Twelve-lead electrocardiography, heart rate, and SpO2 using a pulse oximeter (Ohmeda 3740, BOC Healthcare, Manchester, United Kingdom) were measured continuously.20

Blood Gas Measurement

A catheter was inserted into the brachial artery of the non-dominant arm, under local anesthesia. The indwelling catheter was then fixed in place and the forearm was splinted. For each subject, blood was sampled using heparinized syringes at rest, during unloaded cycling, during loaded cycling at one-minute intervals, and at peak exercise. The blood samples were drawn slowly over an approximately 15 second interval, at the end of each stage of exercise, to include measurements from several breaths to help rid the data of breath-by-breath variability.21 The samples were immediately placed on ice and then analyzed for pH, PaO2, and PaCO2, using a gas analyzer (model 278, Ciba-Corning, Medfield, Massachusetts). The measurement bias (mean difference between measurement and the known value) of the standard solutions with 21.5, 45, and 70 mm Hg of PCO2, using the Ciba-Corning 278 in our laboratory, were −0.9, −1, and −0.7 mm Hg (sample n = 781), respectively. The measurement precisions (standard deviation of bias) of PCO2 for these solutions were 0.9, 1.3, and 1.4 mm Hg, respectively. All blood gas values were calculated at 37°C, since the body temperature change is negligible during a short period of exercise.22 The carboxyhemoglobin level was measured at rest with a spectrophotometric oximeter (CO-Oximeter 270, Ciba-Corning, Medfield, Massachusetts). Whole blood lactate concentrations were also analyzed (1500 Sport, YSI, Yellow Springs, Ohio).

Measurements

V̇O2 (mL/min), V̇CO2 (mL/min), V̇E (L/min), PETCO2, other respiratory variables, and cardiovascular variables were measured. The anaerobic threshold is defined as the level of work just below that at which metabolic acidosis and the associated changes in gas exchange become manifest,23 and was measured using the V-slope method.24 The pH, PaCO2, PaO2, and standard bicarbonate of arterial blood samples were measured and calculated with a blood gas analyzer.

Statistical Analysis

The mean ± SD of each variable is shown unless otherwise specified. Bivariate and multivariable analyses were performed using the subject-specific linear mixed models, which took into account the potential correlations in the PaCO2 within the same individual.25 The predictive values and the coefficients of the fixed effects of the linear mixed models have the same interpretations as those in ordinary linear regression models.

Model Selection

Under the circumstances, with many candidate variables and their interactions, we began with a screening step. First, we performed an all possible subsets ordinary least squares regression procedure, including all demographic, anthropological, and noninvasive clinical measurements as the candidates, and the models provided approximate goodness-of-fit information. This step identified the best ten 3-variable, ten four-variable, and ten five-variable models, according to their performance of adjusted R2 on the predictors.26 In a second step, we then fit a series of linear mixed models, including the 3-, 4-, and 5-variable combinations identified in the first step. The Akaike information criterion, a goodness-of-fit measure, was calculated for each of the candidate models. A smaller Akaike information criterion stands for a better fit to the data.

Internal Validation

To evaluate the predictive ability, a leave-one-out cross-validation predictive error was calculated for each model.27 In brief, the cross-validation predictive error was the square root of the sum of the square of the differences between each case's observed value (eg, the ith case's PaCO2) and predicted value, in which the predicted value was calculated using the equation excluding the case in model building (ie, the ith case was excluded in fitting the equation). One difference from an ordinary leave-one-out procedure is that, since there are 41 independent sampling units (individuals) each with 5–8 measurements, here the leave-one-out procedure left “an individual” out each time, instead of leaving “one observation” out. A smaller cross-validation predictive error stands for a better predictive ability for PaCO2. Thus the models with smaller Akaike information criterion and smaller cross-validation predictive error have priority to be selected. P value < .05 was considered statistically significant.

All the above procedures were carried out using statistical software (SAS 9.2, SAS Institute, Cary, North Carolina, and Origin 4.0, Microcal Software, Northampton, Massachusetts). A special SAS macro was generated for calculating the cross-validation predictive error.

Data Processing

To illustrate the validity of the derived equation for predicting PaCO2, differences between the measured and estimated PaCO2 values during the loaded exercise were compared. Because of the variation among subjects in exercise duration and the number of arterial blood samples that were drawn, we interpolated the multiple PaCO2 values from the start of exercise to the peak of exercise into 100 points for each subject, and then time aligned and averaged the PaCO2 values at each time point of 10% of exercise duration for a group of patients, using Origin 4.0. To test the mean difference between the predicted and measured PCO2, averaging the mean differences over all subjects was conducted. The standard error, 95% CI, and P value to this mean difference were estimated by a linear mixed model to take into account the correlation within the subject.

Results

A total of 41 male patients were enrolled after excluding 6 patients with inadequate data collection for analysis. Most of the patients had a moderate to severe stage of COPD by the GOLD criteria, with moderate air-trapping and mild impairment of DLCO and maximum expiratory pressure (Table 1).

View this table:
Table 1.

Demographics and Lung Function of 41 Men With COPD*

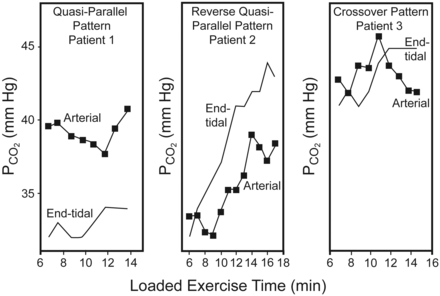
Table 2 provides physiological data regarding subjects at rest and at peak exercise. Forty-six percent of the patients enrolled in this study achieved ≥ 85% of their maximal heart rate predicted, and 92.7% of patients achieved a ratio of V̇E to maximum voluntary ventilation of ≥ 70% at peak exercise. Three patterns of relationship between PaCO2 and PETCO2 in response to exercise were observed: quasi-parallel pattern (n = 34, 83%), reverse quasi-parallel pattern (n = 4), and cross-over pattern (n = 3) (Fig. 1). The patients with the quasi-parallel pattern were older (66 ± 5 y) and had lower SVC (2.6 ± 0.6 L), FEV1 (1.0 ± 0.4 L), peak expiratory flow rate (2.7 ± 1.0 L/s), and DLCO (15.2 ± 4.4 mL/min/mm Hg), by comparison across patients of the 3 patterns (all P < .05).

View this table:
Table 2.

Exercise Data and Arterial Blood Gas Analysis at Rest and at Peak Exercise in 41 Men With COPD*

Fig. 1.
Fig. 1.

CO2 partial pressure measured with arterial blood gas analysis and end-tidal CO2 analysis, in symptom-limited incremental exercise in 3 representative subjects. In the quasi-parallel pattern, both variables increased along with exercise and PaCO2 was higher. In the reverse quasi-parallel pattern, both variables increased along with exercise and PaCO2 was lower. In the cross-over pattern, both variables increased to some extent and then crossed over near the end of loaded exercise.

Univariate analysis revealed that there were 21 variables significantly correlating to PaCO2 (Table 3). After applying multivariable linear mixed regression technique, the 5 models with the smallest leave-one-out cross-validation predictive error were listed in Table 4. Model 1 demonstrated both the smallest Akaike information criterion and leave-one-out cross-validation error. Comparisons between the different predictive models are also shown. In light of the above mentioned criteria, the best predicted equation is: Predicted PaCO2=23.71+PETCO2×(0.9−0.01×DLCO−0.04×VT)−2.61×SVC−0.04×MEP(Equation 1)

View this table:
Table 3.

Univariate Analysis of the Potential Predictors of PaCO2 in Response to Incremental Exercise in COPD (n = 41)

View this table:
Table 4.

Multivariable Models for Predicting Dynamic PaCO2 During Maximum Exercise in 41 Patients With COPD (blood samples n = 306)*

This fitted equation used 306 observations in 41 patients. The Akaike information criterion was 1,099, and the leave-one-out cross-validation predictive error was 6.53. The units of PETCO2 were mm Hg, SVC L, maximum expiratory pressure cm H2O, DLCO mL/min/mm Hg, and VT L.

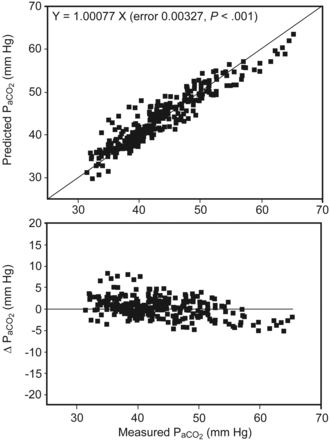
Figure 2 shows the validity of the prediction equation based on the insignificant differences that were observed between the measured and estimated PaCO2 values during the loaded exercise (P > .05). The mean for the measured PaCO2 was 43.2 mm Hg, and the mean for the predicted PaCO2 was 43.4 mm Hg. The mean difference between predicted PaCO2 and measured PaCO2 and its 95% CI were 0.19 and −0.2 to 0.59, respectively (P = .34). Figure 3 shows the validity of the prediction equation, based on the insignificant differences that were observed between the measured and estimated PaCO2 values at each time point of the loaded exercise (all P > .05). The standard errors of the estimated PaCO2 ranged from 0.91 to 1.12 mm Hg.

Fig. 2.
Fig. 2.

Upper panel: Scattergram of measured PaCO2 and predicted PaCO2 using Equation 1. The oblique solid line indicates the line of identity. The oblique dotted line indicates the regression line through zero. Lower panel: Absolute deviations plotted against the measured PaCO2. Each symbol shown represents one blood sample of the 41 subjects. Multiple blood samples were drawn from each subject. ΔPaCO2 is the difference between predicted PaCO2 and measured PaCO2. The differences between each pair of PaCO2 were insignificant (P = .34).

Fig. 3.
Fig. 3.

The PaCO2 measured during the symptom-limited cycling exercise and the estimated PaCO2, using Equation 1 of our study. Data shown are averaged for 41 subjects. The bars show the standard error at the start of loaded exercise, every 10% of loaded exercise, and at the peak of exercise. The differences between each pair of PCO2 were insignificant. None of the differences are significant.

Discussion

End-capillary PCO2 is not equivalent to alveolar PCO2.28,29 It might be anticipated that an individual patient's PaCO2 may not be equal to a more readily measurable PETCO2 under certain physiologic conditions. Some studies in adults,14 including elderly individuals, both at rest and during exercise,11,12 as well as a single study of patients with COPD,13 have shown that the PaCO2 correlates well with PETCO2. However, it has been difficult to predict PaCO2 from PETCO2, due to the increase in CO2 loading to the lung, the inherent inhomogeneous ventilation/perfusion matching, the increased VD/VT, and the cyclic breathing patterns seen particularly in the elderly and in patients with COPD performing exercise. In this study we found that PETCO2 remained the paramount predictor for PaCO2, while the diffusing capacity, the vital capacity, the VT, and the expiratory muscle strength were inversely related to PaCO2 (see Table 4).

Diffusing capacity includes alveolar-capillary membranous diffusing capacity and pulmonary blood volume (ie, pulmonary circulatory capacity). Diffusing capacity for CO is little affected by alveolar-capillary membranous diffusing capacity, except when carbonic anhydrase is inhibited by drugs such as acetazolamide.30 The inverse relationship between DLCO and PaCO2 is believed to be due to a poorer pulmonary circulatory capacity related to COPD. The inverse relationship between vital capacity or VT and PaCO2 is explicitly explained by the Bohr equation. Expiratory muscle strength is negatively related to residual volume,31 and thereby positively related to vital capacity, and therefore inversely related to PaCO2.

By jointly considering these 5 variables and their interactions, the prediction of PaCO2 becomes much better than with any variable alone, because the model fits in terms of lower Akaike information criterion values and has a better predictive ability in terms of lower leave-one-out cross-validation predictive errors.

The carboxyhemoglobin had little effect on the PaCO2 prediction in our study, although it has been reported that carboxyhemoglobin levels increase the difference between PaCO2 and PETCO2 or VD/VT.32 The discrepancies between the 2 studies might be due to the differences in study design. Hirsch et al studied the acute effect of smoking on cardiovascular function of their participants, while we studied the chronic effects of smoking.

It is hard to predict dynamic PaCO2 with PETCO2 alone, because the changes in PETCO2 or PaCO2 occur as a function of exercise intensity and are nonlinear. During a ramp-pattern incremental exercise test in normal subjects, both PaCO2 and PETCO2 increase mildly from the start of loaded exercise to the point of the anaerobic threshold, followed by a leveling-off due to isocapnic buffering, followed by a lower PaCO2 and PETCO2 due to respiratory compensation.33,34 The differences between PaCO2 and PETCO2 are different at different levels of exercise intensity, such as being positive at rest and negative at peak exercise. Based on our findings, another reason that dynamic PaCO2 values are hard to predict with PETCO2 alone is that there are 3 patterns of the relationship between change in PaCO2 and PETCO2 (see Fig. 1).

One may argue that our predictive equation is not the only noninvasive method to yield PaCO2 values. A noninvasive diagnostic tool such as transcutaneous PCO2 monitoring attempted to measure PaCO2 during anesthesia or exercise.2,5,6 The transcutaneous PCO2 measured with CO2 electrodes has been reported to be slow in response time and cannot reflect transient changes noted during different levels of work load exercise or during a 2-min or less incremental exercise evaluation.6,7

The PETCO2 trend of the 9-panel plot is a very useful clue in the diagnosis of right-to-left shunt in dyspneic patients.35 Incorporating the estimated PaCO2 values from our derived predictive equation might make it simpler for a clinician or investigator to detect high ventilation/perfusion mismatch, a right-to-left shunt, or the presence of hyperventilation. Hyperventilation may cause both PaCO2 and PETCO2 to be low, while the high ventilation/perfusion mismatch or right-to-left shunt may cause the PaCO2 to be high and the PETCO2 to be low, thereby augmenting PaCO2 – PETCO2.

The prediction performance of our derived equation and the previously reported data by Liu et al have the same P value (< .001), but our derived equation has a lower standard error of the estimate (0.91–1.12 mm Hg vs 2.8 mm Hg).13 Unfortunately, we cannot compare the R2, due to the different statistical methods, or the calculated PaCO2 values, due to the equations not being provided by Liu et al.13

One study reported that FACO2=FICO2+1.136×V˙CO2/V˙A (where FACO2 is the fraction of alveolar CO2, FICO2 is the fraction of inspired CO2, V̇CO2 is carbon dioxide production, and V̇A is alveolar ventilation), assuming PaCO2 equal to alveolar PCO2 throughout the breathing cycle in young healthy individuals during dynamic exercise.36 They reported that the mean difference and the upper and lower limits of agreement between measured and simulated PaCO2 were −0.004, +0.84, and −0.84 mm Hg, respectively. The authors reported that the V̇A, which involves VD/VT, can only be determined by inserting an arterial catheter and drawing multiple arterial blood samples for calculation.

Study Limitations

A male-only study group diagnosed with COPD prevents application of our findings to the general population. Given the current available data, a multiple regression with the leave-one-out method is a useful way to derive and validate our equation. However, blood gas analysis remains the best way to ascertain EIH, PaCO2 − PETCO2, or VD/VT. To best validate the usefulness of our derived equation, further studies with another patient population are needed.

Another concern is whether or not we increased the sample size while using the interpolation technique to process the data. We interpolated the multiple PaCO2 values because the fitness of each subject might not be identical, and the volitional symptom-limited exercise test was applied so that the exercise durations were different. For comparison at each 10% of exercise time, there were 41 pairs of data: one for measurements and the other for predictions. This technique did not increase the sample size for each comparison. Although the Bland-Altman plot (see Fig. 2) showed an insignificant difference between predicted PaCO2 and measured PaCO2 during the loaded exercise (P = .34), there was a trend that PaCO2 is overestimated if PaCO2 is < 40 mm Hg.

Conclusions

To our knowledge, this study is the first to report equations for dynamic estimation of PaCO2 noninvasively in patients with COPD performing a ramp-pattern exercise test. With a similar average and a small error of the estimate between the measured and estimated PaCO2, we conclude that our predictive equations forecast the PaCO2 accurately and the multiple PaCO2 values estimated from our derived equation can be used to contrast with the PETCO2 trend of a 9-panel plot. The estimated PaCO2 – PETCO2 and EIH can then be readily appreciated.

Footnotes

  • Correspondence: Ming-Lung Chuang MD, Division of Pulmonary Medicine, Department of Critical Care Medicine, Chung Shan Medical University Hospital, No. 110, Section 1, Chien-Kuo N Road, South District, Taichung, Taiwan 40201. E-mail: yuan1007{at}ms36.hinet.net.

  • Drs Chuang and Lin are co-first authors.

  • This study was partly supported by Chang Gung Medical Research Program grant CMRP 443, and by China Medical University Hospital Medical Research Program grant DMRP-96–042. The authors have disclosed no conflicts of interest.

References

  1. 1.↵
    1. O'Donnell DE,
    2. D'Arsigny C,
    3. Fitzpatrick M,
    4. Webb KA
    . Exercise hypercapnia in advanced chronic obstructive pulmonary disease: the role of lung hyperinflation. Am J Respir Crit Care Med 2002;166(5):663-668.
    OpenUrlCrossRefPubMed
  2. 2.↵
    1. Whitesell R,
    2. Asiddao C,
    3. Gollman D,
    4. Jablonski J
    . Relationship between arterial and peak expired carbon dioxide pressure during anesthesia and factors influencing the difference. Anesth Analg 1981;60(7):508-512.
    OpenUrlPubMed
  3. 3.↵
    1. Light RW,
    2. Mahutte CK,
    3. Brown SE
    . Etiology of carbon dioxide retention at rest and during exercise in chronic airflow obstruction. Chest 1988;94(1):61-67.
    OpenUrlCrossRefPubMed
  4. 4.↵
    1. Shade D Jr.,
    2. Cordova F,
    3. Lando Y,
    4. Travaline JM,
    5. Furukawa S,
    6. Kuzma AM,
    7. et al
    . Relationship between resting hypercapnia and physiologic parameters before and after lung volume reduction surgery in severe chronic obstructive pulmonary disease. Am J Respir Crit Care Med 1999;159(5 Pt 1):1405-1411.
    OpenUrlPubMed
  5. 5.↵
    1. Hess DR,
    2. Agarwal NN
    . Variability of blood gases, pulse oximeter saturation, and end-tidal carbon dioxide pressure in stable, mechanically ventilated trauma patients. J Clin Monit 1992;8(2):111-115.
    OpenUrlCrossRefPubMed
  6. 6.↵
    1. Sridhar MK,
    2. Carter R,
    3. Moran F,
    4. Banham SW
    . Use of a combined oxygen and carbon dioxide transcutaneous electrode in the estimation of gas exchange during exercise. Thorax 1993;48(6):643-647.
    OpenUrlAbstract/FREE Full Text
  7. 7.↵
    1. Hoffmann U,
    2. Essfeld D,
    3. Stegemann J
    . Comparison of arterial, end-tidal and transcutaneous PCO2 during moderate exercise and external CO2 loading in humans. Eur J Appl Physiol Occup Physiol 1990;61(1-2):1-4.
    OpenUrlPubMed
  8. 8.↵
    1. Hoffman RA,
    2. Krieger BP,
    3. Kramer MR,
    4. Segel S,
    5. Bizousky F,
    6. Gazeroglu H,
    7. et al
    . End-tidal carbon dioxide in critically ill patients during changes in mechanical ventilation. Am Rev Respir Dis 1989;140(5):1265-1268.
    OpenUrlPubMed
  9. 9.
    1. Raemer DB,
    2. Francis D,
    3. Philip JH,
    4. Gabel RA
    . Variation in PCO2 between arterial blood and peak expired gas during anesthesia. Anesth Analg 1983;62(12):1065-1069.
    OpenUrlPubMed
  10. 10.↵
    1. Russell GB,
    2. Graybeal JM,
    3. Strout JC
    . Stability of arterial to end-tidal carbon dioxide gradients during postoperative cardiorespiratory support. Can J Anaesth 1990;37(5):560-566.
    OpenUrlPubMed
  11. 11.↵
    1. St Croix CM,
    2. Cunningham DA,
    3. Kowalchuk JM,
    4. McConnell AK,
    5. Kirby AS,
    6. Scheuermann BW,
    7. et al
    . Estimation of arterial PCO2 in the elderly. J Appl Physiol 1995;79(6):2086-2093.
    OpenUrlAbstract/FREE Full Text
  12. 12.↵
    1. Williams JS,
    2. Babb TG
    . Differences between estimates and measured PaCO2 during rest and exercise in older subjects. J Appl Physiol 1997;83(1):312-316.
    OpenUrlAbstract/FREE Full Text
  13. 13.↵
    1. Liu Z,
    2. Vargas F,
    3. Stansbury D,
    4. Sasse SA,
    5. Light RW
    . Comparison of the end-tidal arterial PCO2 gradient during exercise in normal subjects and in patients with severe COPD. Chest 1995;107(5):1218-1224.
    OpenUrlCrossRefPubMed
  14. 14.↵
    1. Jones NL,
    2. Robertson DG,
    3. Kane JW
    . Difference between end-tidal and arterial PCO2 in exercise. J Appl Physiol 1979;47(5):954-960.
    OpenUrlAbstract/FREE Full Text
  15. 15.↵
    1. Wasserman K
    1. Wasserman K,
    2. Hansen JE,
    3. Sue DY,
    4. Stringer WW,
    5. Whipp BJ
    . Principles of interpretation: a flow chart approach. In: Wasserman K , editor. Principles of exercise testing and interpretation, 4th edition. Philadelphia: Lippincot Williams & Wilkins; 2005:183-197.
  16. 16.↵
    1. Rabe KF,
    2. Hurd S,
    3. Anzueto A,
    4. Barnes PJ,
    5. Buist SA,
    6. Calverley P,
    7. et al
    . Global strategy for the diagnosis, management, and prevention of chronic obstructive pulmonary disease: GOLD executive summary. Am J Respir Crit Care Med 2007;176(6):532-555.
    OpenUrlCrossRefPubMed
  17. 17.↵
    1. Chuang ML,
    2. Lin IF,
    3. Wasserman K
    . The body weight-walking distance product as related to lung function, anaerobic threshold and peak V̇O2 in COPD patients. Respir Med 2001;95(7):618-626.
    OpenUrlCrossRefPubMed
  18. 18.↵
    1. Benzo RP,
    2. Paramesh S,
    3. Patel SA,
    4. Slivka WA,
    5. Sciurba FC
    . Optimal protocol selection for cardiopulmonary exercise testing in severe COPD. Chest 2007;132(5):1500-1505.
    OpenUrlCrossRefPubMed
  19. 19.↵
    1. Chuang ML,
    2. Lee CH,
    3. Lin IF
    . Using the oxygen-cost diagram in ramp-slope selection for dyspneic patients. Intern Med 2010;49(14):1325-1332.
    OpenUrlPubMed
  20. 20.↵
    1. Chuang ML,
    2. Lin IF,
    3. Vintch JR,
    4. Ho BS,
    5. Chao SW,
    6. Ker JJ
    . Significant exercise-induced hypoxaemia with equivocal desaturation in patients with chronic obstructive pulmonary disease. Intern Med J 2006;36(5):294-301.
    OpenUrlPubMed
  21. 21.↵
    1. Hansen JE,
    2. Casaburi R
    . Validity of ear oximetry in clinical exercise testing. Chest 1987;91(3):333-337.
    OpenUrlCrossRefPubMed
  22. 22.↵
    1. Lee SM,
    2. Williams WJ,
    3. Fortney Schneider SM
    . Core temperature measurement during supine exercise: esophageal, rectal, and intestinal temperatures. Aviat Space Environ Med 2000;71(9 Pt 1):939-945.
    OpenUrlPubMed
  23. 23.↵
    1. Wasserman K,
    2. Whipp BJ,
    3. Koyal SN,
    4. Beaver WL
    . Anaerobic threshold and respiratory gas exchange during exercise. J Appl Physiol 1973;35(2):236-243.
    OpenUrlFREE Full Text
  24. 24.↵
    1. Beaver WL,
    2. Wasserman K,
    3. Whipp BJ
    . A new method for detecting anaerobic threshold by gas exchange. J Appl Physiol 1986;60(6):2020-2027.
    OpenUrlAbstract/FREE Full Text
  25. 25.↵
    1. Verbeke GM
    1. Verbeke GM
    . Estimation and inference for the marginal model; Inference for the random effect; Fitting linear mixed models with SAS; General guidelines for model building. In: Verbeke GM , editor. Linear mixed models for longitudinal data, 2nd edition. New York: Springer Verlag; 2009:41-134.
  26. 26.↵
    1. Kutner M,
    2. Nachtsheim C,
    3. Neter J,
    4. Wasserman K
    . Building the regression model, 4th edition. McGraw-Hill, 2003.
  27. 27.↵
    1. Hastie T
    1. Hastie T,
    2. Tibshirani R,
    3. Friedman J
    . The elements of statistical learning: data mining, inference, and prediction. In: Hastie T , editor. Model assessment and selection, 2nd edition. New York: Springer; 2009:219-257.
  28. 28.↵
    1. Forster RE
    . Can alveolar PCO2 exceed pulmonary end-capillary CO2? No. J Appl Physiol 1977;42(3):326-328.
    OpenUrlAbstract
  29. 29.↵
    1. Gurtner GH
    . Can alveolar PCO2 exceed pulmonary end-capillary CO2? Yes. J Appl Physiol 1977;42(3):323-326.
    OpenUrlAbstract/FREE Full Text
  30. 30.↵
    1. Lumb AB
    . Diffusion of respiratory gases. Nunn's applied respiratory physiology, 5th edition. Edinburgh: Butterworth-Heinemann; 2004:200-221.
  31. 31.↵
    1. Ruppel GL
    1. Ruppel GL
    . Pulmonary mechanics. In: Ruppel GL , editor. Manual of pulmonary function testing, 5th edition. St Louis: Mosby; 1991:39-72.
  32. 32.↵
    1. Hirsch GL,
    2. Sue DY,
    3. Wasserman K,
    4. Robinson TE,
    5. Hansen JE
    . Immediate effects of cigarette smoking on cardiorespiratory responses to exercise. J Appl Physiol 1985;58(6):1975-1981.
    OpenUrlAbstract/FREE Full Text
  33. 33.↵
    1. Wasserman K
    1. Wasserman K,
    2. Hansen JE,
    3. Sue DY,
    4. Casaburi R,
    5. Whipp BJ
    . Physiology of exercise. In: Wasserman K , editor. Principles of exercise testing and interpretation, 3rd edition. Philadelphia: Lea & Febiger; 1999:10-61.
  34. 34.↵
    1. Whipp BJ,
    2. Davis JA,
    3. Wasserman K
    . Ventilatory control of the ‘isocapnic buffering’ region in rapidly-incremental exercise. Respir Physiol 1989;76(3):357-367.
    OpenUrlCrossRefPubMed
  35. 35.↵
    1. Chuang ML,
    2. Chang HC,
    3. Lim KE,
    4. Vintch JR
    . Gas exchange detection of right-to-left shunt in dyspneic patients: report of three cases. Int J Cardiol 2006;108(1):117-119.
    OpenUrlCrossRefPubMed
  36. 36.↵
    1. Benallal H,
    2. Denis C,
    3. Prieur F,
    4. Busso T
    . Modeling of end-tidal and arterial PCO2 gradient: comparison with experimental data. Med Sci Sports Exerc 2002;34(4):622-629.
    OpenUrlCrossRefPubMed
Back to top

In this issue

 

Print
Download PDF
Article Alerts
Email Article
Citation Tools

Jump to section

Related Articles

Cited By...

Keywords