To the Editor:
According to the Society for Simulation in Healthcare, “Simulation is the imitation or representation of one act or system by another. Healthcare simulations can be said to have 4 main purposes – education, assessment, research, and health system integration in facilitating patient safety.”1 Implicit in the concept of simulation is the understanding that the parameters of the simulation reflect realistic values of the system under study. If the model does not accurately represent the system being simulated, then any conclusions about the how the real system behaves based on how the model behaves are suspect.
Simulation for Ventilator Performance Studies
Simulation studies are often used to examine ventilator performance because models of the respiratory system are much easier to understand and experiment with than real respiratory systems (either human or animal). More importantly, models do not vary with time, so the differences observed in measurements are presumed to be related only to performance differences among the ventilators in the study. The simplest model of the respiratory system used for ventilator studies is the single-compartment model, composed of a single-flow resistance and a single-elastic compartment, represented by the equation of motion for the respiratory system (Equation 1).
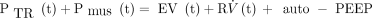[1] where PTR(t) = the change in transrespiratory pressure difference (ie, airway opening pressure minus body surface pressure) as a function of time (t), measured relative to end-expiratory airway pressure. This is the pressure generated by a ventilator during an assisted breath; Pmus(t) = ventilatory muscle pressure difference as a function of time (t); the theoretical chest wall transmural pressure difference that would produce movements identical to those produced by the ventilatory muscles during breathing maneuvers (positive during inspiratory effort, negative during expiratory effort); V(t) = volume change relative to end-expiratory volume as a function of time (t); V̇(t) = flow as a function of time (t), the first derivative of volume with respect to time; E = elastance (inverse of compliance (C); E = 1/C); and R = resistance.
In Equation 1, pressure, volume, and flow are variables, although elastance and resistance are parameters (assumed to be constants). This happens to be the same model used by ventilators that calculate and display R and C values of patients. The compliance of the model is generally assumed to be linear for ventilator performance studies, in the form of C = Δvolume/Δpressure. Resistance is modeled as either linear (R = Δpressure/Δflow) or nonlinear (eg, parabolic). A “parabolic” resistor has a pressure versus flow curve that looks like Figure 1. Note that for a parabolic resistor, the resistance is defined as Δpressure/Δflow at a particular flow value. For example, the resistance of Rp5 (parabolic resistor 5 cm H2O) in Figure 1 is specified as having a pressure drop of 2.7 cm H2O at a flow of 60 L/min, or R = 2.7 cm H2O/L/s, which is about the normal airway resistance of a non-intubated adult.2 This means that the equivalent linear resistance is different for each flow at which it is evaluated. In other words, using a parabolic resistor, the resistive load of the lung model changes as flow changes.
Pressure-flow curves of nonlinear (“parabolic”) resistors used in the Michigan Instruments model 1600 Dual Adult Training Test Lung (modified from the operator's manual). Rp50 = parabolic resistor 50 cm H2O. Rp20 = parabolic resistor 20 cm H2O. Rp5 = parabolic resistor 5 cm H2O.
Most of the studies reporting ventilator performance3,4 use some version of the Training and Test Lung (TTL) simulator (Michigan Instruments, Grand Rapids, Michigan). This device has one or two spring-loaded bellows to model compliance (adjustable spring tension varies compliance values) connected in series with parabolic flow resistors. The TTL is a passive device. To simulate inspiratory effort (Pmus in Equation 1), researchers have improvised by linking the 2 bellows and using one to drive the other by connecting it to a separate ventilator.5 Thus, the larger the tidal volume (VT) and the higher the inspiratory flow of the “drive” ventilator, the higher the simulated inspiratory effort. A good way to quantify the inspiratory effort is by measuring the occlusion pressure (also called P0.1) as described by Boussen et al6
Many recent studies7–9 have used a more sophisticated device: the ASL 5000 lung simulator (IngMar Medical, Pittsburgh, Pennsylvania). This is a computer-driven piston controlled by the equation of motion (Equation 1) to model any value of resistance and compliance for either a single- or double-compartment lung model. It can simulate both passive and active breathing. The latter is accomplished by modeling the Pmus waveform in addition to setting the model resistance and compliance. It is also possible to introduce a calibrated (nonlinear) leak (eg, for evaluation of noninvasive features of ventilators). The ASL 5000 can measure FIO2, making it useful for evaluating devices other than ventilators, such as those used for oxygen therapy.10
Appropriate Selection of Model Parameters
An unfortunate fact about ventilator performance studies is that there is no consistency among researchers regarding the selection of lung model parameters. This makes it impossible to aggregate data across studies. There are some standards that were intended for manufacturers to use for product testing, namely American Society for Testing and Materials (ASTM).11 For example, the ASTM standard specifies both linear and parabolic resistances and linear compliances over a range of values representing adults, children, and infants. These “standard conditions” are shown in Table 1. There are several problems with this standard. First, the values for R and C are not referenced in any way to actual data from human studies, that is, they are not evidence-based. Second, the values are referenced to patient age, not disease type (whereas many ventilator performance studies attempt to simulate disease states like ARDS and COPD). Finally, the standard was withdrawn by the ASTM without replacement in 2004. Researchers are thus left to their own opinions about model parameter values, and few, if any, provide justification for their selections.
Standard Conditions for Ventilator Performance Testing Recommended by ASTM F1100
A recent study in this journal by Boussen et al6 illustrates how questionable selection of model parameters can lead to potentially misleading conclusions. These researchers evaluated transport ventilators using the TTL lung simulator. Their model parameters were as follows: normal: R = 5 cm H2O/L/s and normal C = 100 mL/cm H2O; ARDS: high R = 20 cm H2O/L/s and low C = 30 mL/cm H2O; airway obstruction: very high R = 50 cm H2O/L/s and normal C = 100 mL/cm H2O. The resistances were the parabolic resistors supplied with the TTL. Some of the ventilators were set to a volume control mode with constant inspiratory flow, and some were set to a pressure control mode, which delivers a decaying exponential flow throughout inspiration. The simulator was ventilated with VT values of 300, 500, and 800 mL. One of the outcome variables was volume delivery error (%), although the authors never explained how the error was calculated.
There are several potential problems with the lung model parameters in this study. In the first place, the values of R and C ascribed to normal, ARDS, and airway obstruction disease states are not evidence-based, so we have no way of generalizing the study data to actual use of these ventilators in humans. However, evidence-based data for simulation do exist. For example, Table 2 shows just a few of many studies that could have provided better model parameters. The values for R of 5 or 50 cm H2O/L/s and for C of 100 mL/cm H2O are in particular unrealistic.
Respiratory System Model Parameters Based on Data for Ventilated Patients
Second, because some of the ventilators were operated at constant inspiratory flow and others were operated with variable flow and because nonlinear resistances were used in the lung models, the ventilators were actually subjected to different resistive loads (see Fig. 1). The point is that when comparing the performance of different devices, they should all be subjected to the same experimental conditions. Failing that, some of the variability of the outcome variables might be attributed to the experimental conditions rather than variability in device performance.
Third, the authors observed that one of the ventilators was unable to deliver an accurate VT of 300 mL in the normal condition. This particular ventilator could not deliver 300 mL because it delivers only pressure control modes, and it is designed to deliver no less than 5 cm H2O inspiratory pressure. Hence, the minimum VT it could be expected to deliver to a lung model with a compliance of 100 mL/cm H2O would be 500 mL. This would imply that the ventilator might be inappropriate for use on a normal patient requiring a VT of 300 mL. Indeed, the authors stated that “pediatric patients usually have high compliance and need low VT (< 300 mL).” To see how this might be misleading, we first question the assertion that “pediatric patients usually have high compliance.” Compared with what? Sharp et al17 studied 50 infants and children undergoing elective surgery under general anesthesia. They provide a nomogram for estimating total respiratory system compliance with values ranging from 10 to 80 mL/cm H2O for patients aged 1–18 y. They also provide a prediction equation: compliance (mL/cm H2O) = 2.04 × age (y) + 0.328 × height (cm). If we assume a normal VT of ∼7 mL/kg, then a VT of 300 mL would correspond to a patient weighing ∼43 kg, or ∼94 pounds. Consulting a chart relating age and weight based on guidelines and growth charts provided by the Centers for Disease Control and Prevention and the World Health Organization,18 we see that a male pediatric patient weighing 94 pounds would be ∼13 y old and ∼63 cm tall. Using the prediction equation above, we would thus estimate a pediatric patient requiring a VT of 300 mL to have a compliance of only 47 mL/cm H2O. If Boussen et al6 had used an evidence-based lung model compliance of ∼50 mL/cm H2O, then the ventilator in question would have been expected to deliver a VT down to 250 mL. Thus, it would have “passed the test.”
Fourth, Boussen et al6 also noted that 2 ventilators failed to deliver 800 mL in the airway obstruction model. These ventilators were operated in a pressure control mode. Again, the problem can be traced to unrealistic values for the lung model. Airway obstruction was modeled as having R = 50 cm H2O/L/s and C = 100 mL/cm H2O, which, as noted above, represent excessive values for both parameters compared with actual human data. These values of R and C yield a time constant of 2.5 s. This time constant, in combination with a ventilating frequency of 20 breaths/min, results in an auto-PEEP level of 13 cm H2O. As a result, the ventilator would have to generate an inspiratory pressure change of 62 cm H2O to deliver a VT of 800 mL. Not only that, but a patient with a height of 85 cm has a predicted ideal body weight of 80 kg. Because the maximum pressure limits of the 2 ventilators in question were below 62 cm H2O, they “failed” the test. But implying that these 2 ventilators would not be able to ventilate a COPD patient with an inspiratory pressure of 62 cm H2O and a VT of 10 mL/kg is perhaps an unrealistic and misleading expectation. The fact that the other ventilators could do it may be irrelevant. On the contrary, suppose we use lung model parameters from human data (eg, average of all COPD values; see Table 2), namely R = 22 cm H2O/L/s and C = 56 mL/cm H2O. As a result, a VT of 822 mL is achievable with an inspiratory pressure of only 30 cm H2O, and auto-PEEP is reduced to 4 cm H2O. We come to a different conclusion about ventilator performance: the 2 ventilators that had failed under unrealistic conditions now succeed using evidence-based lung model parameters. Note that the time constant is still long (1.2 s), and thus, VT is highly dependent not only on inspiratory pressure but also on inspiratory time (ie, the inspiratory time setting becomes a potential surrogate for direct VT adjustment in a passive patient).
The calculations for auto-PEEP and inspiratory pressure were performed with a mathematical ventilator-patient simulator that is free to download at https://app.box.com/s/fdayqtzi6v1nm4ycpha6. Simulators like this are quite useful for educational purposes and for simple “reality checks” when trying to interpret study data.
Correction for Gas Condition
Ventilator performance studies that attempt to assess volume delivery error are particularly problematic due to the many factors that contribute such error. Theoretically, the difference between set and measured values for VT can be accounted for by several mechanisms including (1) leaks, (2) inaccurate calibration of either the independent measurement device or the ventilator, (3) volume lost due to compression in the patient circuit, and (4) changes in gas temperature and pressure. Discounting leaks and inaccuracies, we have 2 main factors that need to be accounted for.
Again, the study by Boussen et al6 provides an illustration of how failure to consider these complications can lead to ambiguous results. Although these authors did not provide the equation they used to calculate percentage error for volume delivery, one version is as follows: error (%) = [(set VT − measured VT)/measured VT] × 100%. With this equation, if the set VT was less than the measured volume, the error would be negative, and we would say the set value underestimates the true value.19 Boussen et al6 reported volume delivery errors ranging from −30 to +53%, but we do not know what a negative error indicates without the equation used to calculate it.
Volume lost due to compression would tend to make error positive (ie, set volume is larger than measured volume). Some ventilators have gas compression compensation, meaning that the volume delivered from the ventilator's output control valve will be adjusted above the set value. Inaccuracy of the compensation algorithm contributes to volume delivery error. Some ventilators use flow sensors at the airway opening, which could potentially make compression compensation algorithms unnecessary. Boussen et al6 did not note which ventilators in their study did or did not have compression compensation algorithms. Nevertheless, any error due to compression is a “legitimate” error in the context of the study.
What is more concerning, however, is the error introduced as a result of the researchers failing to account for temperature and pressure. Ventilator performance studies typically do not use humidifiers because of the additional complexities involved. However, just as some ventilators have compression compensation algorithms, some also have compensation for gas expansion due to the change from atmospheric temperature and pressure dry (ATPD) conditions leaving the ventilator to body temperature and pressure saturated (BTPS) in the lungs.20,21 Going from ATPD to BTPS can increase the VT by as much as 12% (Table 3).22 Thus, ventilator correction algorithms attempt to decrease the volume coming out of the ventilator compared with the set value if the set value is displayed in BTPS. In the study by Boussen et al6, some of the ventilators had correction algorithms for BTPS, and some did not. However, the authors did not note this, nor did they assure us that the final values for volume error percentage took such compensation into account. For example, the Dräger Carina and Oxylog 3000+ (Dräger Medical, Lübeck, Germany) ventilator operator's manuals state that volume and minute ventilation displays are corrected for BTPS. The Hamilton-T1 and Hamilton-C1 (Hamilton Medical, Reno, Nevada) manuals say that pressure, flow, and volume measurements are based on readings from the flow sensor, and they are expressed as BTPS. I do not know how the other ventilators handle this issue. Boussen et al6 did not state whether their measurements were corrected for BTPS conditions but only that the pneumotach calibration was checked with a Super Syringe. This suggests that their measurements may have been values closer to ATPD then BTPS. For example, if the operator set a VT of 500 mL, and the ventilator displayed the set value as BTPS, then a measurement made assuming ATPD conditions would indicate only 445 mL. Thus, if the experimenter was not aware of the ventilator compensation, he might incorrectly report an error on the order of +12%. Note that if a ventilator did not compensate for compressed gas but did compensate for BTPS, the errors would tend to cancel each other.
Tidal Volume Changes Due to Changing Environmental Conditions
Conclusion
Lung simulators are very useful for ventilator performance evaluation studies. However, care must be taken to select lung model parameters that are evidence-based and reflect actual human lung conditions. Otherwise, the results of the simulation cannot be generalized to actual ventilator use and may in fact be misleading. Furthermore, when reporting volume delivery error, appropriate corrections must be applied relative to ventilator compensation algorithms that may be in effect for compressed gas and ATPD versus BTPS conditions.
Footnotes
The author is a paid consultant for Invacare, Philips, Covidien, Breathe Technologies, Dräger, IngMar Medical, Hamilton Medical, and ResMed.
- Copyright © 2014 by Daedalus Enterprises
